Attention
Self Attention
$$ \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V $$ 简要理解Q,K,V: Q * K 得到相似度权值,对V做加权平均。 与数据库查询非常相似,可以将 Query 看作是搜索查询,Key 看作是数据库索引,而 Value 则是实际的数据库条目。注意力机制的核心是对于给定的 Query,计算其与所有 Keys 的相似度,然后用这些相似度对 Values 进行加权求和,得到最终的输出。
先来理解 $\operatorname{softmax}\left({XX^T}\right) X$:
$X$为输入,维度为n×512 (n为token数量,512为Embedding的维度)
${XX^T}$:矩阵X的每一行向量代表改token。经过embedding之后的结果。${XX^T}$得到一个新方阵,保存了每一个行向量与自己和其他行向量内积运算的结果。 内积的含义表征一个向量在另一个向量上的投影,值越大两者相关度越大,eg:向量夹角90度时,两者线性无关。词向量是词在高维空间的数值映射。词向量之间相关度高–>在关注词A的时候,应当给予词B更多的关注。
$\operatorname{softmax}\left({XX^T}\right) $: Softmax用以归一化,归一化后,得到方阵的每个行向量之和为1,用于加权平均。
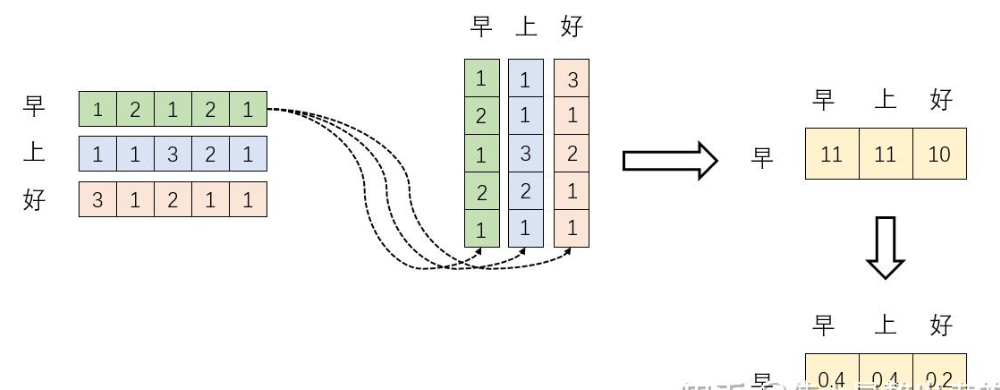

$\operatorname{softmax}\left({XX^T}\right) X$: 以 $\operatorname{softmax}\left({XX^T}\right)$的一个行向量举例。新的行向量就是"早"字词向量经过注意力机制加权求和之后的表示。
${\sqrt{d_k}}$: 缓和并稳定梯度
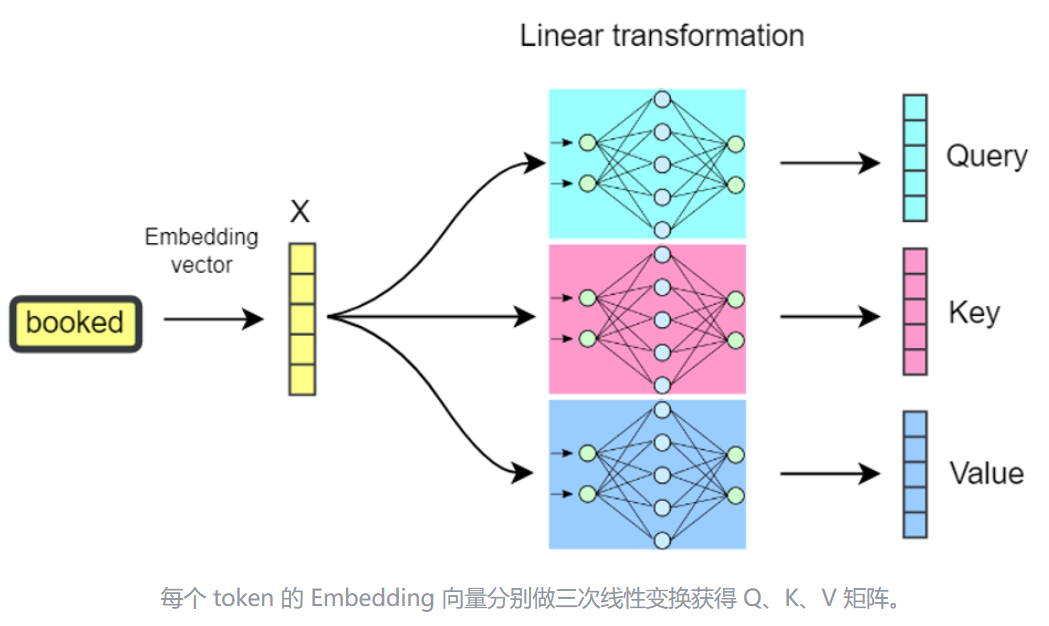
Q, K, V: 为矩阵X与权重矩阵$W^q$,$W^k$,$W^v$的乘积,本质上都是X的线性变换。权重矩阵是Transformer在预训练阶段时,从亿万预料学习的结果。
时间复杂度计算
Background
- 矩阵乘的时间复杂度:假设A(n×m),B(m×p), 则A×B时间复杂度为O(n×m×p)
- softmax 公式 $$\sigma(z_i) = \frac{e^{z_{i}}}{\sum_{j=1}^K e^{z_{j}}} \ \ \ for\ i=1,2,\dots,K$$
- softmax 时间复杂度: 取决于输入,例如向量长度为n,softmax需要对每一个元素进行指数运算O(1),然后求和O(n),最后对每个元素除法操作O(n), 整体时间复杂度位O(n)
- 假设输入长度为n,embedding嵌入维度为d
self-attention时间复杂度
- Q(n×d)矩阵和K(d×n)矩阵的点积:$O(n^2d)$
- softmax函数:矩阵大小为(n×n), 故复杂度为$O(n^2)$
- attention sorce(n×n)与V(n×d)矩阵相乘:$O(n^2d)$
总时间复杂度$O(n^2d)+O(n^2)+O(n^2d)=O(n^2d)$
[使用KV Cache后,计算复杂度可以降低到O(n⋅d),显著减少了计算量。]
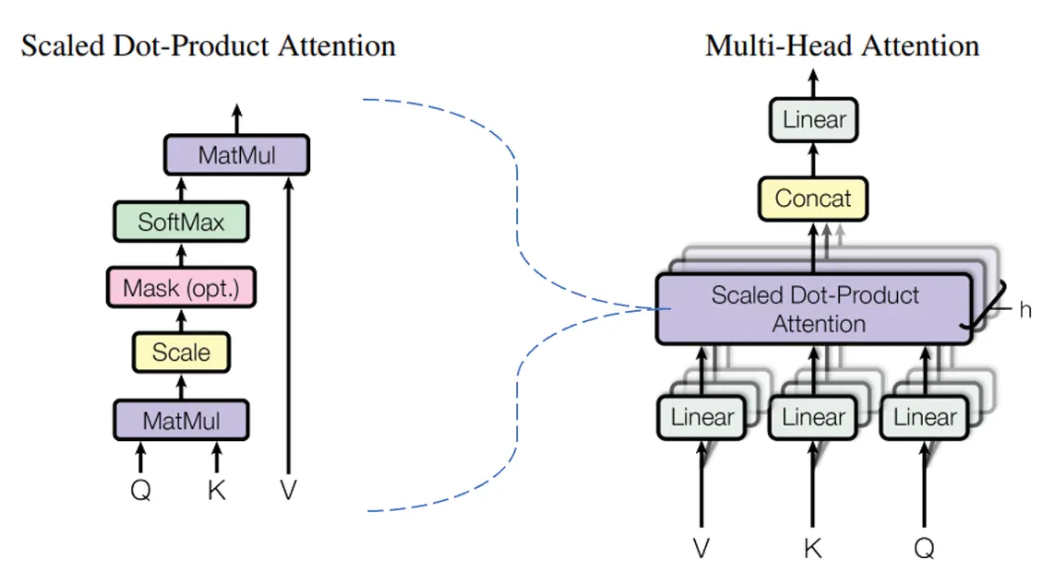
Multi-Head Attention
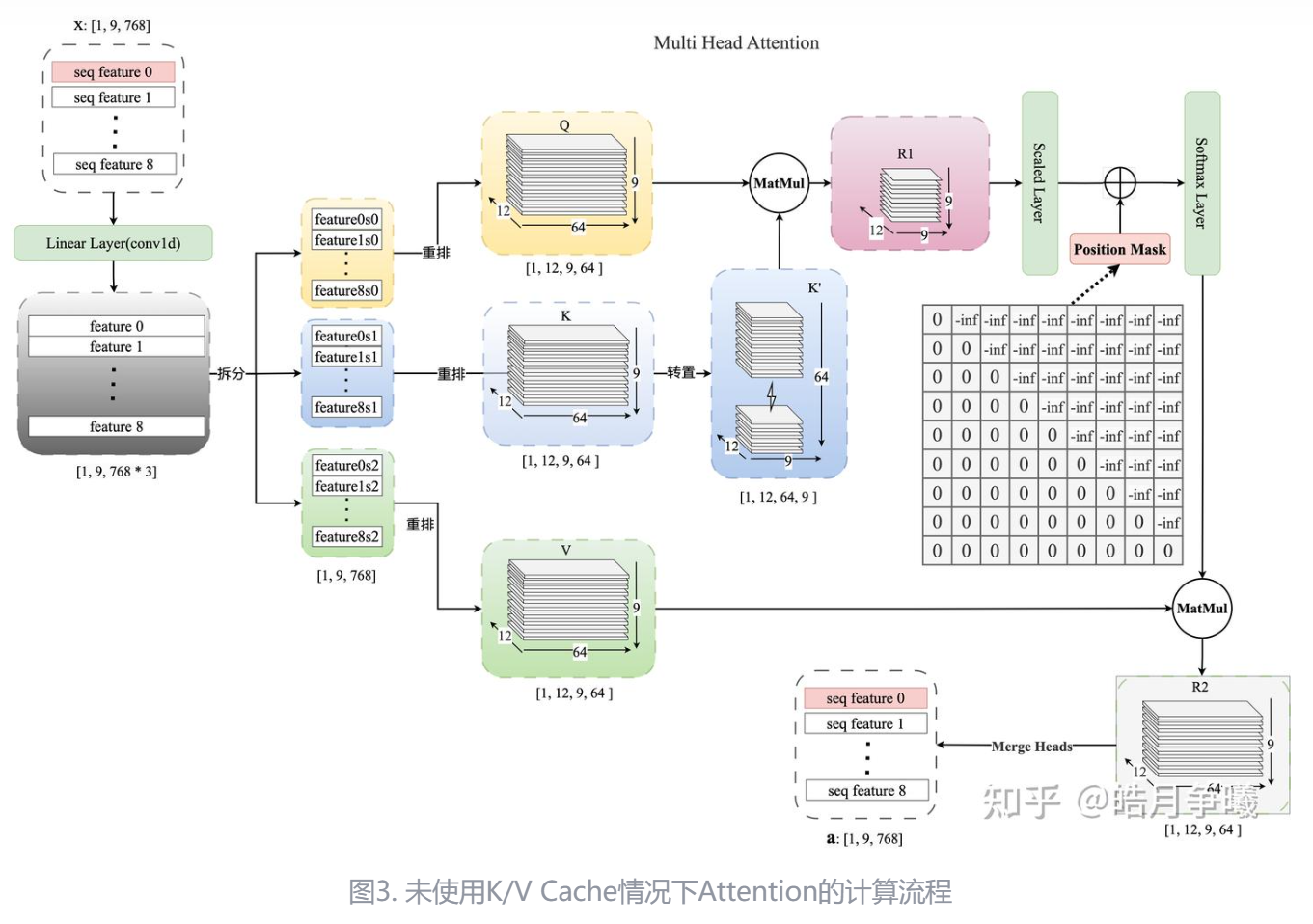
在实际操作中,权重矩阵$W^q$,$W^k$,$W^v$通常被拆分成多份,如8个。相当于把token的Embedding向量通过线性变换,投射在某个细分语义逻辑子空间(语义、语法、上下文逻辑、分类逻辑等等)的方式降维分解成 8 个细分的 Embedding 向量(n⨯512->n⨯64),并产生对应的不同QKV组合,以进行不同 head 的 Attention 计算。只拆分权重矩阵,不拆分X。

Multi-head Attention 多头注意力机制运算结束后,系统会通过 Concat 方式把 8 个子进程的结果串联起来,并通过另一个线性变换的方式恢复为原 Embedding 的 512 维的向量长度。 分出 8个头 head 时,并非直接在物理层面上八等分切割 512 长度的 Embedding 到 64 长度,而是通过线性变换得来的 8 个具有独立语义逻辑的子空间“小Embedding”。所以在 Multi-Head 运行结束后,在 Concat 后,我们需要通过矩阵再做一次线性变换,即再把 8 个小的语义逻辑子空间有机地整合成一个总体的 Embedding。
公式 其中的Q,K,V是为了表示其作用,其实都是X:
$$
\operatorname{MultiHead}(Q, K, V)=\operatorname{Concat}\left(head_1,…,head_h\right) W^0,
\
\text{where } head_i = \operatorname{Attention}\left(QW_i^Q,KW_i^K,VW_i^V\right)
$$
Example: 假设一个输入的句子只有两个 token,那么运算过程如下:
假设 $d_{model}=512, h=8, d_k=d_q=d_{model}/h=64, d_v=100$ ($d_{model}$位transformer中所有子层和embedding层的输出维度, h位ehad数 d_v可以等于d_q也可以u不等于)
- 输入序列为2个token,转化为2个Embedding向量,即X矩阵(2×512)
- 训练好的权重矩阵$W_i^Q$和$W_i^K$形状为512×64,它们把X分别线性转化为 2×64的$Q_i$和$K_i$矩阵
- $Q_i$和$K_i^T$做矩阵乘法,得到2×2矩阵,然后经过softmax,得到矩阵$Y_i$(2×2)
- 预训练好的权重矩阵$W_i^V$形状为512×100,它把X线性转化为2×100的矩阵
- 然后,用$Y_i$的2×2 矩阵与$V_i$的2×100矩阵做Attention运算(相乘,得到结果$Z_i$ 2×100
- 以上的进程做8次,并把$Z_i$矩阵Concat到一起,得到一个2×800的矩阵
- 最后,训练好的权重矩阵$W^O$是形状为800×512。它把$z_{Concat}$线性变化成一个 2×512 的新矩阵$Z$, 与初始输入的矩阵$X$具有完全一样的形状,即 2×512。此时,可以理解为$X$做过一次 Multi-Head Attention 机制后产生的变体。
时间复杂度计算
- 假设有m个head,每个维度为d/m=h
- 时间复杂度主要还是点积,可以理解为m次Q矩阵[n×h]和K矩阵[h×n]的点积:$O(mn^2h)=O(n^d)$
KV Cache
以GPT为代表的Decoder-Only自回归语言模型在生成每一个新的 token 时,接受所有之前生成的 tokens 作为输入。然而,对于这些先前生成的 tokens,每次生成新的 token 时都需要重新计算他们的表示,造成了计算浪费。
引入KV Cache,将之前生成的tokens 对应的 key-value 对存储起来。当生成新的 token 时,直接从 KV Cache 中取出这些已经计算好的 key-value 对,再把当前token的key-value做一个连结在进行计算,从而避免了KV的重复计算。
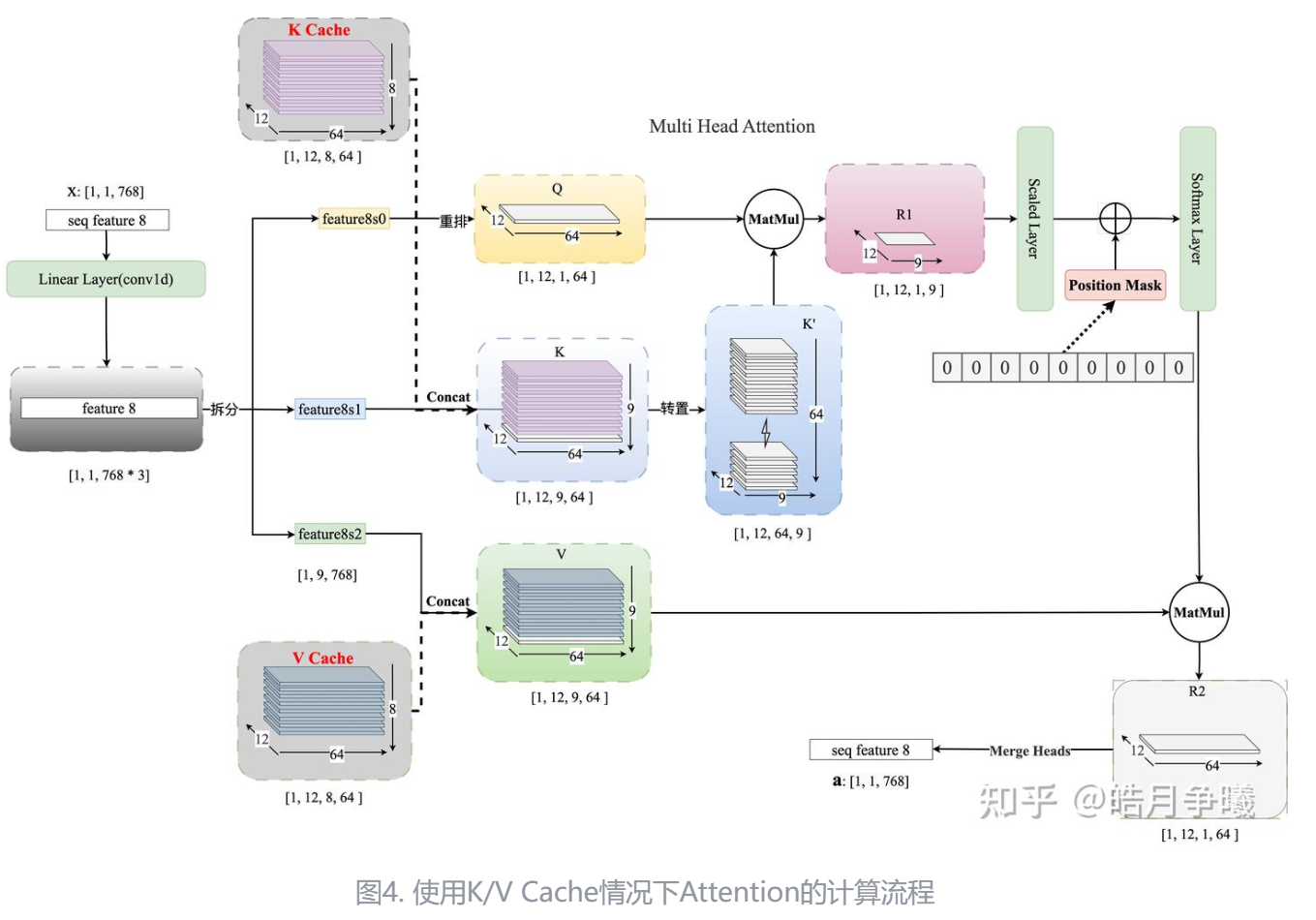
使用KV Cache包含以下两个步骤:
- 预填充阶段:计算第一个输出token过程中,Cache为空,计算时需要为每个 transformer layer 计算并保存KV cache,在输出token时Cache完成填充;
- KV Cache阶段:在计算第二个输出token至最后一个token过程中,此时Cache是有值的,每轮推理只需读取Cache,同时将当前轮计算出的新的Key、Value追加写入至Cache;
显存占用
假设:
- 批处理大小$b$
- 输入序列的长度为$s$
- 输出序列的长度为$n$
- 精度$p$,指模型的每个参数的字节数,如FP16精度下每个参数2字节,则p=2
- 模型decoder layer的层数$l$
- 模型隐藏层维度的大小$h$ (对于每个输入 token,模型会计算一个 Key 向量和一个 Value 向量,其维度均为h)
那么KV cache的峰值显存占用大小为 $2 \cdot b \cdot (s + n) \cdot h \cdot l \cdot p$